Abstract

This paper analyzes both differential privacy and data de-identification. While differential privacy seeks to create differentially private data through the use of mathematics, data de-identification seeks to anonymize data in such a way that it cannot be re-identified at a later date. In addition, we analyze the challenges of both methods of approaching privacy, including the possibility of data re-identification and verification of privacy, before addressing possible methods of mitigating these challenges. Such methods include setting outer bounds of data, utilizing shared central databases with larger datasets, and grouping data into fewer data category buckets. The merits and benefits of both methods are discussed as well.

I. AN INTRODUCTION TO DIFFERENTIAL PRIVACY

Differential privacy can be defined as a mathematical method of approaching privacy in which data is considered differentially private once it is impossible to say conclusively whether a data output was part of an original dataset [1]. In some cases, this is accomplished, at least in part, through the use of a five-number statistical summary (minimum, maximum, lower quartile, upper quartile, and median), in addition to variance, mode, and mean. In other cases, the mathematics can be more complex, using combinatorics and calculus-based calculations.

The primary goal of differential privacy centers around an idea that a quantitative value to privacy risks provides a method of relative comparison that is objective instead of subjective. In matters related to privacy, risk is arguably the most important metric to consider. However, historically, risk has been difficult to quantify, and is often presented as a binary metric. Thus, accumulated risk can be calculated using differential privacy, which requires amending our previous definition to include the “parameters (‘epsilon and delta’) that quantify the ‘privacy loss’ – the additional risk to an individual” [1]. In this sense, we could say that differential privacy offers a thorough view of privacy risks.

For purposes of this analysis, we will define epsilon as an “error term in regression/statistics; more generally used to denote an arbitrarily small, positive number” [2]. Each epsilon can be run for multiple iterations. We will define delta as “the probability of privacy leakage” [3]. Conceptually, this is probability of data being identified to a data entry in the original dataset, and mathematically it can be defined in terms of M and K, where K represents the individual of whom the identity is being concealed and where M is the corresponding entry in the differentially private database. As the probability of privacy leakage (delta) approaches zero, we consider the data to be reasonably private and the possibility of personal identification to be low.

Additionally, as delta approaches zero, we can infer several general possibilities about either the dataset or the effectiveness of differential privacy method used.

First, one possibility is that the database is sufficiently large and any clear outliers have been removed from the dataset. In this case, the size of the database has made the possibility of individual identification difficult if not impossible. This stems from the principle that more individuals in a dataset overall will result in more data entries in each data category bucket, leading to many similar looking records.

A second possibility is that the number of data category buckets is small, also making individual identification more difficult. As an example, we can consider data category buckets for grouping data record owners by age. In cases where we use full date of birth (MM/DD/YYYY), we can assume that there are approximately 32,940 data category buckets (366 possible dates * 90 possible age buckets). If we instead use only year of birth, the number of data category buckets gets reduced to only ninety. In this example, the possibility of personal identification is significantly reduced.

A primary goal of differential privacy is to achieve a guarantee of privacy. However, importantly, this is accomplished only under specific conditions. One of these conditions is that only data within a certain standard deviation from the arithmetic mean is included in the differentially private dataset. This ensures that any outliers are removed from the original dataset, given that outliers are much easier to re- identify at a later date. In cases where the distribution of data category buckets is close to evenly distributed, we can utilize a bell curve to model the exclusion of data outliers, although the specific distributions and area under the curve will vary, sometimes significantly, in response to the size and nature of the dataset.

For purposes of this analysis, we will utilize the standard equation for the graph of a bell curve, which is:

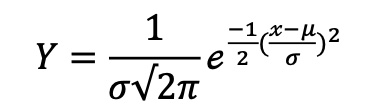
The graphing of this equation will lead to the production of the graph presented in Figure 1 (below), which represents the standard bell curve under normal distribution.

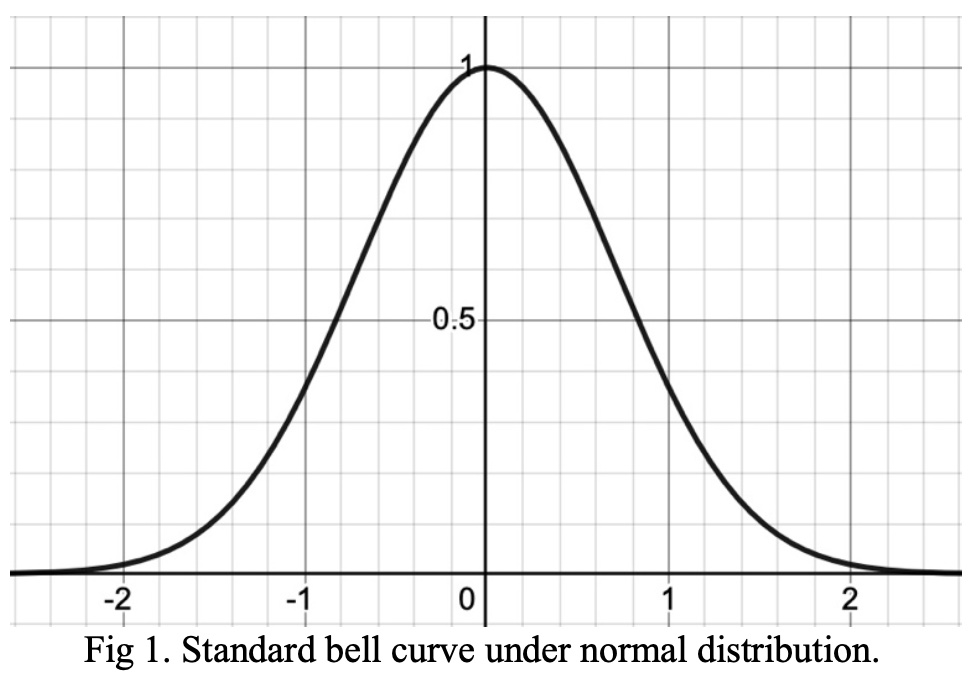
Removing the outliers from this data set requires that we exclude the outer bounds on both sides (minimum and maximum). This can be seen in the shaded portion of Figure 2 (below).

Using a bell curve is only possible in cases where there is a normal distribution of data. Further, for small datasets, the probability of a naturally occurring normal distribution of data is low. That said, standardization (or Z-score normalization) may still be possible, resulting in a mean of 0 and a standard deviation of 1 [4]. There are various methods of systematically removing outliers in cases where the distribution of data is not normal or standardized.

II. AN INTRODUCTION TO DATA DE-IDENTIFICATION

Understanding the merits and challenges of data de- identification requires an understanding of the fundamental meaning of data privacy. NIST defines privacy as “assurance that the confidentiality of, and access to, certain information about an entity is protected” [5]. The word ‘assurance’ is important to the NIST definition of privacy, because it implies some form of either guarantee or verification that ‘certain information’ is confidential. Theoretically, this is accomplished with differential privacy. However, it is also worth considering methods of achieving either a guarantee or verification of privacy using traditional data de-identification, without the mathematic approach offered by differential privacy.

Providing a guarantee of privacy or verification of privacy is challenging because of an inherent conflict between the ability to verify data and the privacy of data, which we can consider as the absence of personally identifying information. We can represent this conflict graphically, as seen in Figure 3 (below); however, it is important to note that this correlative conflict will seldom result in linear one-to-one trade-offs.

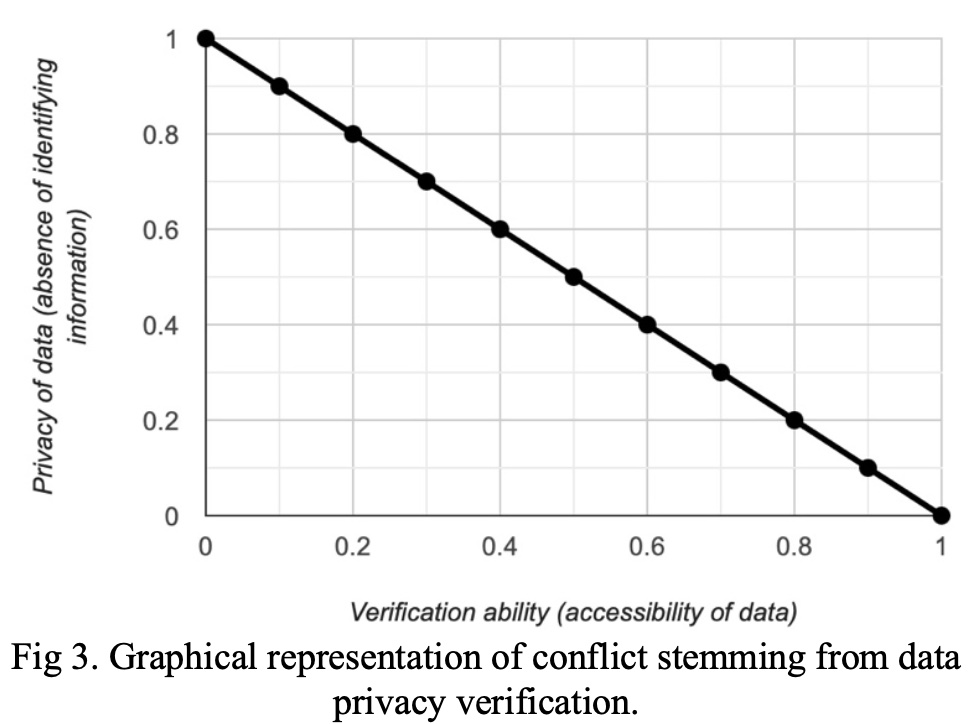
While the purpose of Figure 3 is to provide a simplified visual approach to a relatively complex challenge, the graph fails to take into account the impossibility of perfection. Theoretically, this graph indicates that when verification is impossible, data is one-hundred percent private. However, in practice this would never be the case. The data would be visible, for example, to whoever is granted admin access to the database. In theory, this may be close enough to perfect privacy that the impossibility of perfection is ignored. However, in practice, there are cases where a guarantee of privacy can only be made with a reasonable degree of certainty as a result of the impossibility of perfect, and the resulting risk would need to be indicated, regardless of risk likelihood. Likewise, the endpoint at which verification ability is equal to one-hundred percent is also impossible, given that true verification would require an eyewitness account. For example, in an examination of voter records, we could say that verification is possible if one- hundred percent of voter data is released, including which candidate a particular voter voted for in a certain election. However, short of contacting each voter and verifying the voter record lines up with the vote they made at the polling booth, we cannot verify one-hundred percent of this information. Even if we are able to get in contact with every voter, we have to take into account the possibility that a voter forgot whom he/she voted for (i.e., if the voter were to have dementia or Alzheimer’s). This is to say that to be completely certain of the integrity of the data, we would need to observe the voter making the vote with our own eyes. Thus, perfect verification is also impossible. The impossibility of perfection is taken into account in a theoretical manner in Figure 4 (below).

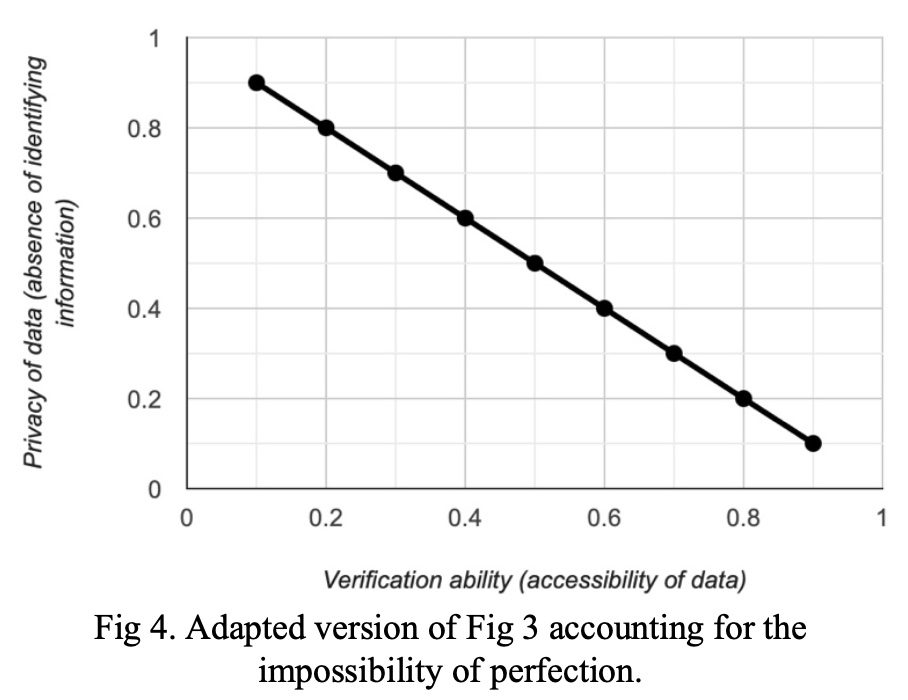
Regardless of the challenges noted in this graphical representation, it is still worth considering the trade-off between privacy and verification ability. De-identifying data implies we have chosen to value data privacy above verification ability, and are trying to move toward the y-axis of Figure 3 or Figure 4. Perhaps the easiest way of handling de-identification is to remove all identifying information before the data is processed and saved to the database. However, without an identifier, a key question is raised. How do we ensure data integrity without verification?

Without an identifier, duplicate records are almost inevitable. For example, if a data record is being generated every time a visitor accesses a particular website page, we can assume that at some point in time the same individual will visit the page more than once. In this case, the database will contain two duplicate records, which may skew analytics or other forms of data analysis.

One method of avoiding this problem is attempting to remove duplicate entries by looking for entries that look similar, or the same. This could be done by analyzing the mathematical probability of the data entries matching based on how closely data fields match. This is mathematically represented using the equation below, where P = probability.

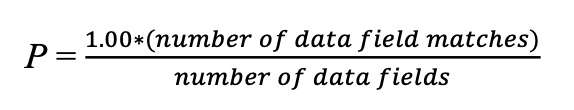
It is important to note that the accuracy of this method of removing duplicate entries will increase in cases where the data fields are sufficiently unique. For example, if the only data field being recorded are location of website visitor, it will be difficult to determine duplicates. However, if data fields such as demographics (including date of birth), device type, browser type, etc. are recorded as well, identifying duplicate entries by using a probability analysis becomes more accurate. We also have to consider the possibility that some data fields may change over time. For example, an individual may access the same website from multiple different cities. Each of these records would be included as duplicates in the database, even if a probability analysis is done.

In light of this, the obvious solution may be including a unique identifier, but that can pose privacy challenges. For a unique identifier to be truly unique, we would need a method of ensuring that the identifier corresponds to one and only one data record. There are many mathematic and computational methods of doing so; however, they all share one commonality. This commonality is the possibility of data re-identification.

III. POSSIBILITY OF DATA RE-IDENTIFICATION

As datasets contain more fields, the possibility of individual identification becomes more likely. Through Table 1 and Table 2, we can see an example of two data records that each contain the same data fields, and the differences in ease of re- identification. Table 1 is below.

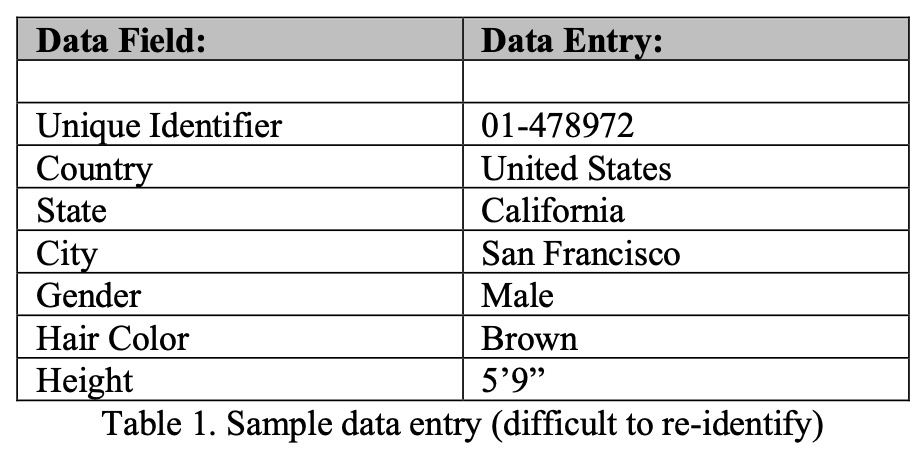
While Table 2 (below) contains the same data fields as Table 1 (above), it would be much easier to re-identify the individual represented by the Table 2 data record for several reasons. First, notice that the individual is located in a very small city with a population of 16,416 people [6], instead of a major city (San Francisco, CA). Second, notice that the hair color changed from brown to red, with only two percent of the population having red hair [7]. Finally, the height is far outside the normal distribution of height among men. When we consider the red hair color and height in the scope of the small population, re-identifying the data record is far more likely than is the case in the first data record.

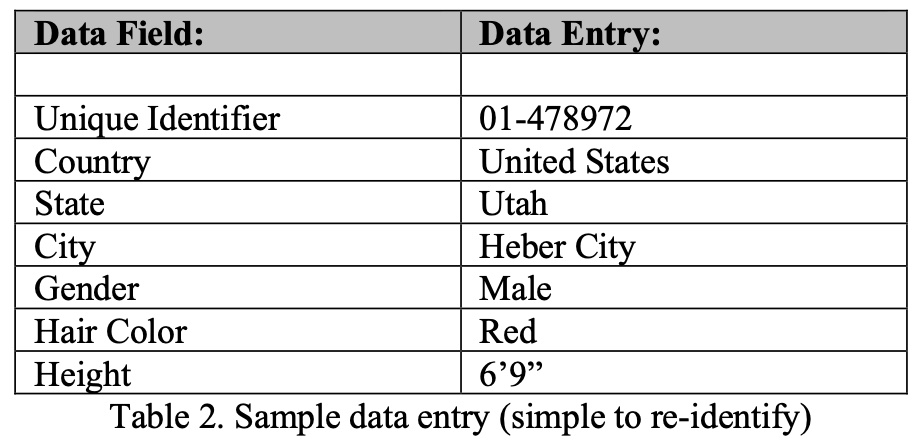
The addition of even more data fields, such as year of birth, would make re-identification even easier. Thus, the collection of the same data fields may pose different levels of risk to different individuals. One method of addressing this is to remove outliers, similar to the bell curve method shown in the differential privacy portion of this paper. In some cases, removing the outliers will have minimal ramifications. However, for some use cases, this may have significant implications. For example, a hair care brand may track hair color closely. For this business, removing a rare hair color (i.e. red) could have negative business implications, including loss of revenue.

[1] “Differential Privacy,” Harvard University Privacy Tools Project. [Online]. Available: https://privacytools.seas.harvard.edu/differential- privacy. [Accessed: 15-Mar-2023].

[2] “Greek letters common usages alpha - university of new mexico,” University of North Mexico. [Online]. Available: https://www.unm.edu/~ckbutler/ps541/MathNotation.p df. [Accessed: 15-Mar-2023].

[3] M. Aitsam, “Differential Privacy Made Easy,” 2022 International Conference on Emerging Trends in Electrical, Control, and Telecommunication Engineering (ETECTE), 2022.

[4] C. Liu, “Data transformation: Standardization vs normalization,” KDnuggets, 12-Aug-2022. [Online]. Available: https://www.kdnuggets.com/2020/04/data- transformation-standardization-normalization.html. [Accessed: 15-Mar-2023].

[5] “Privacy - Glossary,” NIST CSRC. [Online]. Available: https://csrc.nist.gov/glossary/term/privacy. [Accessed: 15-Mar-2023].

[6] “Is Heber the best Utah City for your business?,” Utah Demographics. [Online]. Available: https://www.utah- demographics.com/heber-demographics. [Accessed: 15-Mar-2023].

[7] H. Wood, “27 Hair Color Statistics, Facts & Industry Trends,” Holleewood Hair, 28-Dec-2022. [Online]. Available: https://www.holleewoodhair.com/hair-color- statistics/. [Accessed: 15-Mar-2023].